Solving Freudenthal’s Impossible Problem
Alice declares “I am thinking of two whole numbers between 3 and 100. I have told their sum to Sam, and their product to Polly.”
Sam says to Polly “You don’t know the numbers.”
Polly replies “That was true, but now I do.”
Sam responds “Now I do too.”
Determine the numbers.
This Blog Post
I figure I might as well lead with the problem, so that you know exactly what you’re getting into. The above is the Freudenthal Problem, as I first heard it. Now I’ll outline what you are going to read here.
In this blog post, which is my entry to the 2nd Summer of Math Exposition, I’ll be diving into this puzzle. I’ll display a visual approach to the solution, which reveals the information being exchanged by the cryptic clues. Then I’ll change the problem, getting rid of the upper bound. I’ll share an efficient algorithm that reveals solutions. I’ll define Freudenthal’s Comet and show a graph of the first couple hundred thousand values. Answers will lead to new questions, and from there to discussion of deeper mathematical principles. Finally, I’ll share my own progress on a yet-unanswered question: are there infinitely many solutions?
Target Audience
My goal is for this post to be accessible to mathematicians and non-mathematicians alike. You should be able to get something out of this blog post, coming in with little more than curiosity. If the problem sounds impossible to solve, and you want a walkthrough, good! If you have heard of this puzzle already and can see the connections to number theory, good! From my fruitless searching in the past, I expect that what I am writing is the single most complete piece of literature on this problem, at least in the direction that I am taking it. I hope everyone reading is able to find something fascinating hidden in Freudenthal’s Impossible Problem.
History
Who is Freudenthal and what does he have to do with Alice, Sam and Polly?

Hans Freudenthal was a Dutch mathematician, and a pioneer of “Realistic Math Education”. In his perspective, a student should start with a question, and develop math as an approach to solving it. It’s not surprising then, that he asked himself this curious math question, one which uncovers tremendous depth. It was published in Dutch in the Netherlands in 1969.
This question was picked up by American popular science writer Martin Gardner, who wrote a Mathematical Games column in Scientific American. Here, Gardner gave it the name “The Impossible Puzzle”.
There are several versions of the puzzle. The lower bound may be 1 or 2 or 3, and the upper bound adjusted accordingly to give a unique solution. When I encountered it, as an extra credit problem in a Discrete Math class led by the wonderful Art Benjamin, the lower bound was 3.
Common between all versions is the dialogue between Sam and Polly. Somehow, “you don’t know” is the key piece of information that solves the entire mystery.
Alice
To begin, we need to think carefully about Alice’s role in the puzzle. Her line sets up the problem for the reader, but the fact that she declares it to everyone, including Sam and Polly, is important. This line tells us exactly what each party knows.
Alice declares “I am thinking of two whole numbers between 3 and 100. I have told their sum to Sam, and their product to Polly.”
Let’s review the information.
Two numbers between 3 and 100
I like to visualize pairs of integers as points in the plane. In the animation below, we begin with all the points consistent with the premise.
It doesn’t really matter their order, since sum and product are both commutative. So we could arbitrarily pick one of them to be bigger, reducing the square to a triangle. I like the look of a triangle with its right angle in the lower right, so I pick for the x-coordinate to be the larger one.
Every point defines a possible choice Alice may have made, and we can write the corresponding sum and product next to it.
Lines of constant sum
With this picture, we can add a line connecting points which have the same sum. It goes diagonally.
Sam knows which line the answer is on, because he was told the sum. The points along a line are regularly spaced, so if a line goes through more of the triangle, it will have more points. Almost all of the sum lines contain multiple points (the only exceptions are the ones at either end, 6 and 200).
Curves of constant product
We can similarly add a curve connecting points which have the same product, which is a hyperbolic curve.
Unlike sums, it is much less clear how many points are on one of these curves. There are curves like the one for 1729, that pass through a significant amount of the bounding triangle, but only hit a single point. Alternatively, there are curves like the one for 720, which go through many points.
We can make a table of how many curves exist, sorted by the number of points they contain. Of our whole triangle’s worth of points, here is how they break down:
There’s a clear relationship with factorization, but we will get to that later. Right now, it’s purely visual. There are curves, and some of them pass through fewer points than others.
Polly knows what curve the point is on.
Polly
If Alice told a product to Polly, and it matched one of the 1786 curves with only one point, then Polly would know the two numbers immediately. This, as well as many claims to follow, is because we assume that Sam and Polly are “perfect logicians”. If there is something that they could deduce from the available information, then they know it.
To reflect that fact, for all of the 1786 curves with only one point, we can go ahead and mark that point a different color. A point is red, if Polly knows the numbers already.
“You don’t know”
Now it’s time for the actual dialogue of the problem. Based on only what Alice has said, anyone can construct the image above.. including Sam! And with the extra piece of information that Sam has, he can say to Polly: “You don’t know the numbers”.
How could Sam know this? Well, let’s look at the lines. Some of them pass through only red points, or a mix of red and white. If the sum is one of these, then there exists a way for the two numbers to be a red point. And if that were true, Sam wouldn’t be able to say his statement with confidence. Instead, the sum must be a line that contains only white points. Only if all points are white, could Sam deduce that Polly cannot possibly know the two numbers.
Put another way, Sam may have stated “you don’t know the two numbers”, but this is informationally identical to the statement “my sum is a line that contains only white points”.
Aha!
That is actually quite a lot of information. The fact that it is stated as “you don’t know”, is deceptive. Obviously to you or me, any person telling us that we don’t know something, is unhelpful. It’s because Sam and Polly are perfect logicians, and aware of so much context, that the statement is powerful in the way it is.
So now, let’s remove some points. We will remove any red point, as well as any point that shares a line with a red point. By doing this, we have removed a lot of points.
Down to just 152 points, on 10 lines!
If we rebuild the table from before, but restricted to the points that remain, the values are different. We have a new set of points which have become alone on their curves. I’ll color them green this time.
Finding the answer
“Now I do”. “Now I do too”.
To be careful with the logic here, let’s look at what these statements mean. Green points are points with exactly one associated curve. Polly currently knows the numbers, so her point must have gone from white (which was all of these points) to green. Furthermore, it needs to be the only point on its line to have become green. That way Sam will be able to say he knows the numbers too.
As a result, there is exactly one answer. One point left, that is uniquely green on its line.
The numbers are 16 and 13. Their sum is 29. Their product is 208. This is the solution to the impossible problem.
Not So Fast!
If you wanted to be done here, you absolutely could be. This would get you the extra credit on the Discrete Math homework. But to me, simply knowing the answer is unsatisfying. What is special about 13 and 16? If I had a computer spit out this answer for me, or read it on someone else’s blog post, I would not walk away believing that I understand something about math, that I didn’t understand yesterday.
I want to generalize. And here there are at least two different ways you might generalize the problem.
The Logician’s Way
To the logician, this is a filtering problem. Start with a large set of possibilities, and write a set of conditions that picks out exactly one of them.
I’ve seen versions of the “you don’t know” problem, that don’t start with numbers. Instead they have something a little more contrived, which allows a dialogue that looks more like this:
“You don’t know”
“Correct”
“You still don’t know”
“Correct”
“You still don’t know”
“Correct”
“You still don’t know”
“Aha! Thanks, now I know”
Each stage of this problem communicates a slightly different filter, based on the updated version of both players’ knowledge. Figuring out a premise where this works, is a fun logic puzzle in itself, and delivering the result to friends will make them properly puzzled.
But I don’t like contrived premises. In fact, I don’t even like that the Freudenthal problem gives an upper bound…
The Number Theorist’s Way
The purity of the integers has always enticed me. I love games on grids, where each location sits alone, distinct from its neighbors. I have played (and blogged about!) a game with divisors and sums, where strategy ventures into the realm of number theory. Although I did take a number theory course in college, I wouldn’t consider myself a number theorist by profession. I work with physics and software. But to me, there’s a clear “Number Theorist’s Way” to generalize the Freudenthal problem. It retains the exact roles of Sam and Polly, the representatives of sum and product. But it opens up the lid on the integers.
The Infinite Impossible Problem is the exact same, but with the upper bound removed, and without the requirement for a unique solution.
Alice declares “I am thinking of two whole numbers greater than or equal to 3. I have told their sum to Sam, and their product to Polly.”
Sam says to Polly “You don’t know the numbers.”
Polly replies “That was true, but now I do.”
Sam responds “Now I do too.”
Classify all possible pairs of numbers.
Tackling the Infinite
A natural first question would be: how do we start? This problem breaks at the very first step of our previous approach. We can’t hold onto the set of all possible pairs of numbers.
Well, but we can. It’s an infinite set, but we can describe it simply. We just need to use inequalities, instead of listing every possibility somewhere in our computer’s memory.
Lines and Curves
As shown, every single line and every single curve, goes from the top of our now-infinite wedge of space, to the bottom. In doing so, it touches finitely many grid points, never infinite. So even though we the reader need to look at infinity, both Sam and Polly have an upper bound in mind of how large the numbers can be.
In fact, let’s focus on that idea.
What are Sam’s and Polly’s upper bounds?
Let’s assume that the solution is some point. Based on that point, Sam would be told the corresponding sum and Polly the product.
Sam could, in theory, consider all the possible products consistent with the sum he was just told. And from there, all the possible sums consistent with those products. And the products for those sums, and so on..
Polly can do the same, starting with her product. Each layer deeper will reel in more points from the infinite. But we don’t need to go on forever.
The shadow of a solution
The idea here is to assume that any single point is a solution, and then figure out how many other points we need to bring in, to either confirm this or find a contradiction.
Let’s carefully trace back the conditions from before, in the reverse order. The sum has to have one green point, so all other points need to be white. White points come from connecting that sum to other sums via a shared product. Those sums are in turn defined by all of their products having at least one more point on them, to avoid containing red.
Thus, for any point, we need to expand along sum → product → sum → product. Two iterations apiece, and all the points picked up along the way. These are the only points that we will ever have cause to consider. And to make the animation a fair bit simpler, we can just trace out the highest single line or curve at each step. That final curve will bound a finite set of points, and it doesn’t change the problem if we include all of them instead of only the ones that can contribute to the solution.
And so, every point has an associated “shadow”. Pick a point, compute its shadow, and then run the original filtering problem on that shadow. If it is logically sound, we have found a solution to the infinite impossible problem.
(16, 13)
The first triumph of using shadows, would be finding one solution. Shown below is an animation that proceeds exactly the same as before, but where the initial points come from the shadow of (16, 13). There are several “solutions” in the end, but we built this shadow to support (16, 13) only. We need other shadows to make claims about other points. The entire point of this construction is to determine strictly whether (16, 13) is the only green point on its line, after the filtering is over.
And it is. (16, 13) is a solution to the infinite impossible problem.
The next solutions
It’s not efficient, but we can go point by point, assume it’s a solution, build its shadow, and then either reach a triumph or a contradiction. If we do this, the next time we triumph is at (73, 16). And then (133, 16), (163, 16), (127, 64), (193, 16)..
An aside:
You might wonder why (73, 16) isn’t a solution to the original problem, with bounds at 100. After all, both numbers are in the allowed range. However, when we introduce an upper bound, we remove points from lines and curves that go past the bound, impacting the filtering steps. For a specific example that contradicts (73, 16), we can consider the product 1908. Without an upper bound, this product has 7 points on it. But 6 of them have one factor larger than 100. By setting the upper bound to 100, we remove those 6 points, so the remaining point at (53, 36) becomes red. Then 89 can’t be Sam’s sum, so (73, 16) cannot be the solution.
The start of a trend?
Having an algorithm is great! It lets us generate data, to start making hypotheses. Feel free to try to make hypotheses about the solutions using the data so far. I find it’s a good way to get invested in a problem. For example, 16 and 64 are both powers of 2, and either one or the other appears in every solution so far. The other number is usually prime, but 133 is not..
Unfortunately, our algorithm is not efficient, and my laptop cries trying to go further. If we want more data, we have to work smarter. It’s time to use some more math.
Prime Factorization
Every integer has a prime factorization. When finding two factors that multiply together to reach a given product, you can look at all of the product’s prime factors, and divvy them up. In the visualization below, I’ve taken each prime and turned it into a block.
Every unique way of divvying up the primes, while obeying the bounds, is a point on Polly’s curve. But we have to be specific about uniqueness. I’ll always put the larger factor on the left, and the primes that are being stacked together in decreasing order bottom to top.
Bounds
When there are both upper and lower bounds, it’s hard to imagine coming up with a clear set of rules. But without the upper bound, it’s quite a lot simpler! We just need to be sure that we put enough in either stack, to reach the lower bound of 3.
Counting prime factors
Let’s try to get a complete picture of all possible products. We will break products into 5 classes:
• powers of 2
• powers of some other prime
• 2 distinct prime factors, one of which is 2
• 2 distinct prime factors, both of which are odd
• 3 or more distinct prime factors
Powers of 2
Whenever our product is a power of a prime, then all of the blocks we are stacking are the same size. When that prime is 2, we need two blocks in each column to be able to pass the lower bound. Accordingly, the smallest power of 2 that Polly could ever be told, is 16. There’s only one way of stacking for 16, as well as for 32.
After 64, every power of two can be stacked in multiple ways.
Powers of some other prime
p is a prime that is not 2, so it is odd and it is always large enough to satisfy the lower bound on its own.
In this case, the blocks are still all the same size. But now it only takes a single block in either column to reach the lower bound. Like before, there are two cases with only a single option – two copies and three copies. Everything larger has multiple valid stacks.
2 distinct prime factors, one of which is 2
This is probably the most interesting type of product for the problem. First note that if we just have the prime and 2, then we can’t pass the lower bound. So at least one of them needs to be repeated. But in both cases, if you repeat one of them once, you are left with only one option.
If you repeat either one of them further, it becomes possible to find multiple valid stacks.
2 distinct prime factors, both of which are odd
In this case, we are stuck only if neither prime repeats. If either one of them repeats, we have multiple valid stacks.
3 or more distinct prime factors
Finally, all of the other numbers will have multiple valid stacks. This is the same idea as before, we put something different at the bottom of each column, and the rest is free to bounce back and forth. We don’t need to worry about whether one of them is 2, because we have three distinct primes. At least two of them will be greater than 2, and so those can sustain the column on their own.
Correspondence
This analysis is complete, every single product will take one of the forms shown above. Looking at the results leaves us with 7 different ways Polly would know the factors. For each of them, we can find the corresponding sum. A few of these sums are just numbers, but most of them are formulas in terms of odd primes p or q.
For the Infinite Impossible Problem, Sam’s statement “you don’t know the numbers” is equivalent to the statement “my sum cannot be written as any of the above”.
So, let’s find out what is left. We will start with a major conjecture in number theory.
Goldbach’s Conjecture
Goldbach’s conjecture is among the most well-known unsolved problems in number theory. It states that every even number greater than 2 can be written as the sum of two primes.
If Goldbach’s conjecture is true, then the two forms p + q and 2p carry a lot of weight. Between them, every single even sum is ruled out. This makes including 8, 12, and p2 + p completely redundant.
This simplifies the final column above. Assume Goldbach’s conjecture, and just replace the even entries in the sum column with “even”. There will be a red point somewhere on those lines no matter what.
Aside: do we believe Goldbach’s Conjecture to be true?
Goldbach’s conjecture is one of those statements that is notoriously difficult to prove, but very simple to amass evidence for. One famous visualization is known as Goldbach’s Comet. In Goldbach’s Comet, we count how many ways a given even number can be written as the sum of two primes. For example, 10 is 5 + 5 and 7 + 3, so the count for 10 is 2. Then we plot that count, vs the original number. The result looks spectacular.

Goldbach’s conjecture is equivalent to the statement that this graph never hits zero. There aren’t any zeros at the left, so we would need to find one somewhere far away on the right. Since the graph is consistently trending upward, it feels like a pretty safe claim that there aren’t any. I will continue this blog post by assuming that Goldbach’s conjecture is true, which allows us to make Sam’s statement into rather simple logic.
The set S
With all this machinery, we can reformulate Sam’s statement “you don’t know the numbers”. I’ll define the set S to be every number which:
• Is odd
• Is not 3p for some prime p
• Is not 4 + p for some prime p
This precisely dodges all of the conditions above. In the context of the infinite impossible problem, both Sam and Polly can come up with the set S on their own, before Sam speaks. They don’t necessarily need to call it the same thing. But it is of obvious importance to the problem. Sam’s statement tells Polly: “My sum is in S“.
Given a potential sum, it is easy to check whether it is in the set S. For example: 1000003. It’s odd, and it isn’t a multiple of 3. The only thing to check is whether you get a prime or composite number when you subtract 4. And 999999 is clearly divisible by 9, so it’s composite. Therefore, 1000003 is in S. And in a very simple way, adding more zeros in the middle can prove that the set S has infinitely many sums in it.
Progress
Just as before, this filters our options from being defined by an inequality, to laying on specific diagonal lines. The image can’t capture infinity, but the set S can.
And as before, due to this filter, Polly knows she now must find a factorization of her product whose factor sum lives in S.
An Algorithm
With an improved understanding of the first step, we can generate solutions using far less computing power. I used an ancient method known as the Sieve of Eratosthenes to build out a lookup table for S that filled a good fraction of my computer’s available memory.
Then, starting with the smallest sum in S, the algorithm goes through each point, and computes its product. A bit set holds onto which products have been seen exactly once. There are two kinds of values in that set – ones which we might still encounter again, and ones that we definitely cannot ever encounter again (because the remaining products are all larger). In the animation below, these are gray and green respectively.
After running the algorithm, we know exactly how many points on the first several lines, turn green from Sam’s statement. Any line with exactly one green point on it, corresponds to a solution to the infinite impossible problem.
Limitations
While this does give us genuine solutions, it’s still an algorithm that has to run, and we can’t give it infinite space or time. But in terms of efficiency, it is far better than using shadows. The C++ code that I used to implement this algorithm is able to work with sums out to several billion when run overnight.
To interpret the results, we need to understand at what point we are “missing something” from the finite amount of space we have on a computer. If we have products stored up to 10 billion, then the smallest pair of numbers we can write which falls off the end, is 100000 x 100001. Their sum is 200001, so that’s the sum where our data is no longer sufficient. The largest sum whose points are actually green, is the largest we can validly calculate solutions for. It goes something like the square root of the amount of bits of memory on the computer.
More data!
On the flip side, if we can say that everything out to 200000 is guaranteed complete, then we can collect all of the solutions to the infinite impossible problem with a sum less than 200000. Not too shabby! If you made a hypothesis before, it’s time to refine it.
There are 1869 solutions with sum less than 200000. 1313 of them have a power of two as their even number, but 556 of them do not. The first example of a solution without a power of two, is (448, 61). 16 and 4096 are the most common values to appear. The smallest even number belongs to the single solution (137233, 4) that contains 4.

Of the odd numbers, a majority are prime, but 51 (around 3%) of them are composite. This isn’t new, (133, 16) was already an example of a composite odd number showing up in a solution.
Over half the odd numbers end in 3, although 1, 7 and 9 also sometimes appear as the final digit. There aren’t any 5s. The smallest odd number to appear is 7, as part of the solution (16384, 7). The two most common odd numbers are 883 and 41113, but that’s with a paltry 5 solutions apiece.
Having data also lets us do something even cooler..
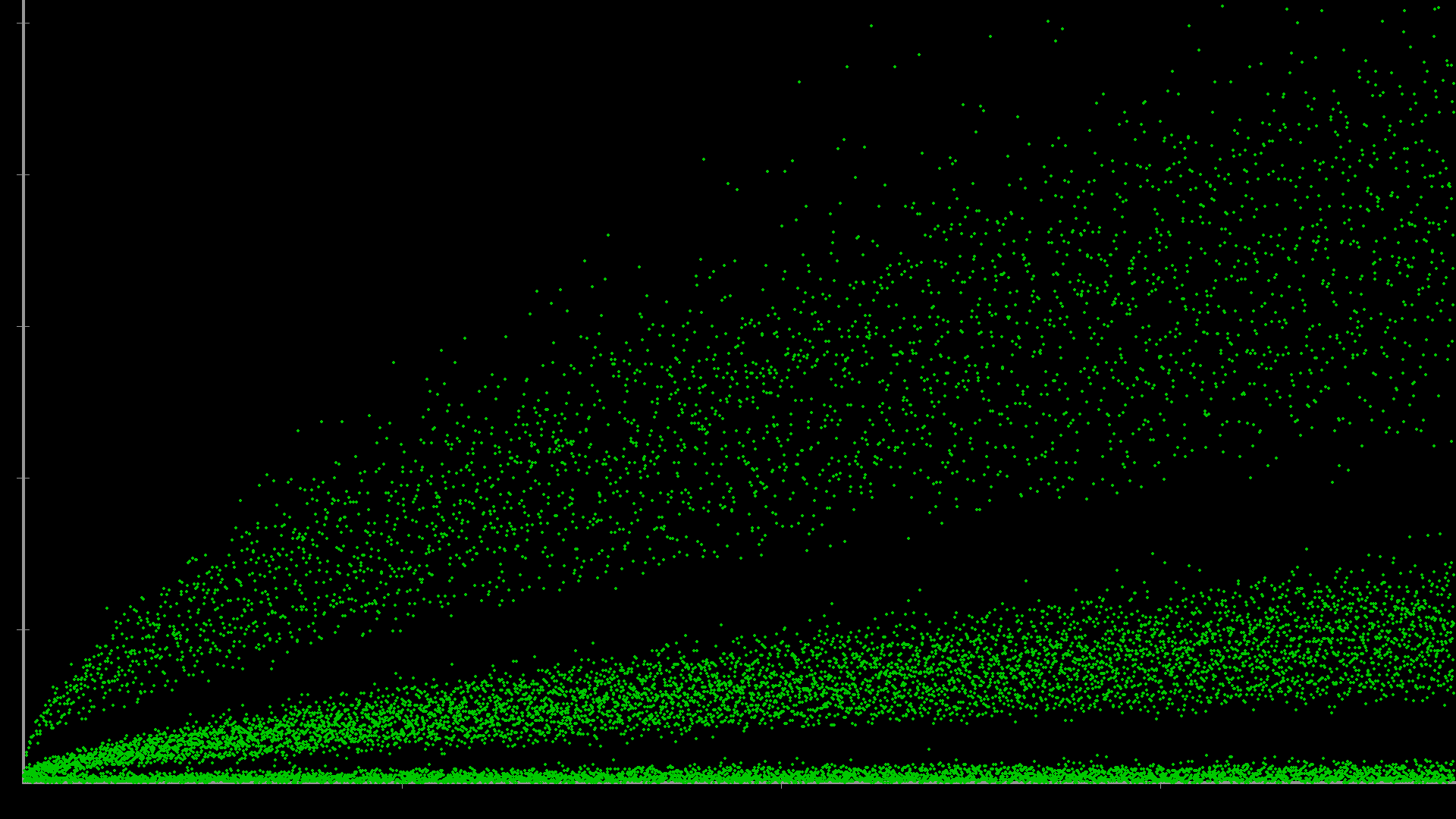
Freudenthal’s Comet
Inspired by Goldbach’s Comet, I found a way to visualize the behavior of the Freudenthal problem, on the last step before Sam says “Now I do too”. At this point in the dialogue, we know that there’s a set S, and some of the points on the corresponding lines have turned green. Since Polly knows the numbers, it’s the green points we care about. How many green points are on each line?
A graph of this function out to a sum of 40000 is shown below. I call this graph Freudenthal’s Comet.

Isn’t that amazing?
Interpretation
Freudenthal’s Comet is the graph of a function, I’ll call it F(s). The domain is the set S defined previously. That is to say, we can only ask about F evaluated at a number in S. On anything else it doesn’t have a value at all.
F(s) plays out the infinite impossible problem assuming that Sam’s sum is s, but without specifying Polly’s product. After Polly says “now I do [know the numbers]”, F(s) spits out the number of different products where that is possible.
If F(s) = 1, then Sam has enough information to say “Now I do too”. Accordingly, we the solvers are able to find a solution for every s where F(s) = 1.
If F(s) > 1, the final line of dialogue is impossible. If F(s) = 0, which sometimes happens, then Polly’s line in the dialogue is impossible. The only consistent pairs of numbers, which are solutions to the infinite version of Freudenthal’s impossible problem, match exactly onto sums where F(s) = 1.
But why does Freudenthal’s comet have that shape?
This is the number theory question of the hour! F(s) encodes basically everything about the Freudenthal problem. If we can understand this function, we can answer the infinite impossible question at a greater depth than any algorithm ever could. So let’s finally give up on algorithms, and try to do some plain old math. We want to understand the conditions that give green points, and convert them into statements about F(s).
Points that will always be green
To begin, I want to highlight all the following points. These are all the points that have one coordinate a power of two, and the other coordinate a prime number.
Every single one of them is green, and that’s for good reason. We can prove it! Going back to the block stacking, we can reason through our candidate factorizations.
There’s only one way to make an odd factor, and that’s by leaving the prime in a column by itself. If you have 2s on both sides, your factors will both be even, and so the sum will be even. The fact that these even factors exist means that Polly doesn’t know the numbers right away, but as soon as Sam tells her that his sum is in S, she can eliminate them immediately. S takes only odd sums. So Polly will figure out the numbers, meaning the point is green.
So that does a good job of motivating things like (16, 13). Those points will be green, even if the line they are on has very few green points for some reason.
Rarity
Powers of 2 are comparatively rare. If you count up to N, you will pass log(N) powers of two, while you will pass something closer to N / log(N) primes. Don’t worry that the logs here have technically different bases, they are close enough that the argument is valid. The point is that as our sum s gets large, expressing s as “power of two plus prime” is not more common. A careful analysis shows that we expect there to be the same number of points which are made from one prime and one power of two, on enormous sums, as on small sums. Not the same proportion, the same total count. That number is “about 2”, obviously with some room for being more or fewer.
But, they’ll always be green, so that’s something.
Points that will never be green
We can also figure out a rule that prevents points being green. This happens whenever we can find a separate factorization for its corresponding product, and prove that the factor sum is also in S.
In order to say something about infinitely many points, we want to write an expression, instead of a single coordinate pair. So that means we are asking about whether an expression is in S. Before we dive into specific expressions derived as factor sums, let’s make sure we understand the idea of proving an expression is in S.
The simplest expression to prove
When I say expression, I mean something like 6x + 1, where x is any whole number. We can actually prove that this expression is in S for all x > 1. It’s definitely odd, and it’s definitely not divisible by 3. Additionally, when we subtract 4 from it, we get a multiple of 3. That will be a composite number unless it is exactly 3, which is the only prime multiple of 3. And since those were our 3 checks, we’ve done it.
Thus for x > 1, we’ve shown 6x + 1 is in S. That’s every number in the arithmetic progression 13, 19, 25, 31, 37, etc..
Next I’m going to try to walk through the problem, using expressions for the two numbers themselves. From when I first encountered the problem, I didn’t think this would be useful. But having done it, I will give a bit of a teaser.. we get impressively far!
Expressions all the way
Pick an arbitrary point from the image where all the lines in S remain. We know that this point corresponds to two numbers, their sum is an odd number s, and that s – 4 is composite.
That’s not nothing. If we know that the sum is odd, then we know that one of the summands is even, and one is odd. As before, order doesn’t matter. We will write the odd summand as a, and the even summand as 2kb, where b is odd.
About k
k is the number of factors of 2 in the even coordinate. This has a fancy name, the “2-adic valuation”, and there’s an associated Greek letter and a lot of jargon. I don’t want to subject you to that, especially if you haven’t encountered it before. For this blog post, I will call it k, and it is the only way I will use k, so it will remain unambiguous. Every point in the entire grid has a k value, and that k is very important.
For about half of our points, k is 1.
For a quarter, k is 2; for an eighth, k is 3. And so on.
It’s not exact for any finite image, but in the infinite limit this proportion becomes more and more correct. Hopefully this makes sense, since when you divide an even number by 2, you just get a number. Half of the time it will be odd, in which case you’re done, and half of the time it’ll be even, in which case you repeat the process.
A specific alternate factorization
Our point is (a, 2kb), and our sum s = a + 2kb. Our product is 2kab. a is definitely at least 3, while b is some odd number, possibly 1.
To make our lives easier, let’s make a couple assumptions. b does not equal 1 or a. Both of those will mess up the following chain of logic, and we would need to treat them separately. For now I’ll just let the corresponding points be “unknown”. Maybe they are green, maybe not. It’s a small enough proportion of the points, that we don’t need to spend our effort on it right away. From here on, b and a are separate odd numbers and both are at least 3.
What that means, is that we are guaranteed the ability to move all of the 2s from sitting atop b, to sitting atop a, giving us a new odd sum.
This is by no means the only other factorization, but it’s an important one. If we can prove that it is also in S, that’s enough to ensure that no points on the curve for 2kab are green. We are now focused on determining when s‘ = b + 2ka is in S. I’ll call s‘ the “alternate factor sum”.
Modular Arithmetic
Let’s try to additionally figure out when s‘ is a multiple of 3, and avoid that. Note that modulo 3, multiplying and dividing by two are the same thing. So when we move a 2 from one factor stack to the other, we are performing the same operation on both stacks. You can verify that as a result, the sum s‘ is only ever divisible by 3, if s itself was divisible by 3.
We are hunting for solutions to the impossible problem, so we are free to define a bunch of properties, and then look for s which satisfy those properties. For our task here, we will require that s is not a multiple of 3.
Useful Algebra
The next question is whether s‘ – 4 is composite. If our new number s‘ is not 4 + p for some prime p, and we’ve already shown it to be odd and not divisible by 3, then it must be in S. So let’s write it, as well as add and subtract s in two ways. Each result will be a useful expression for later, so I’ll let them play out in parallel.
To determine when s‘ – 4 is composite, we will look at the greatest common divisor (GCD) of the part that depends on k, and the part that depends on s. For reasons that connect to other areas of mathematics, I’ll call the left expression “Mersenne”, and the right expression “Fermat”.
Mersenne
Mersenne numbers are those of the form 2k – 1. You may have heard of Mersenne primes, which are simply Mersenne numbers which are prime. These are famous because there is a very powerful algorithm for determining whether a Mersenne number is prime, which is used by projects like GIMPS, the Great Internet Mersenne Prime Search. This project is responsible for the largest 8 prime numbers we know.
Important to our discussion of the Freudenthal problem, a Mersenne number 2k – 1 can only ever be prime if k is prime. 2ab – 1 is always divisible by 2a – 1. With a prime exponent, 2p – 1, there still can be factors, (for example 211 – 1 = 2047 = 23 × 89). But 2p – 1 cannot be divisible by other, smaller Mersenne numbers.
The expression s‘ – 4 that we want to find a factor for, is some multiple of a Mersenne number, plus s – 4.

As our next requirement on s, we want s – 4 to share some nontrivial factor with certain Mersenne numbers. When that is true, s‘ will be in S, and so every single point on the line s that has the corresponding value for k, will vanish.
What does that mean?
Let’s start with the simplest example of a Mersenne number: 22 – 1 = 3. I claim that whenever s – 4 is divisible by 3, then none of the points with k = 2 can ever be green. Data backs this up:
This comes because when we write s‘ – 4, both of the terms are divisible by 3. This means that s‘ takes the form 6x + 1, which we proved before was in S. And since both s and s‘ are in S, then Polly can’t have 2kab as her product, because she wouldn’t be able to say she figured out the numbers.
Accordingly, the points are not green.
Furthermore, because 2ab – 1 is always divisible by 2a – 1, we know that 3 is a divisor of 2k – 1 for every even k. So when s – 4 is divisible by 3, we lose k = 4, 6, 8, etc as well. That’s less and less impactful, but still worth remembering.
By the same vein, we can look at 23 – 1 = 7. Whenever s – 4 is divisible by 7, we lose of all the k = 3, 6, 9, etc.
Limitations
We aren’t able to predict not-green-ness for that many points. Mersenne factors cannot ever eliminate k = 1, because 21 – 1 = 1 is not a “nontrivial divisor”. Showing s‘ – 4 is divisible by 1 does nothing to prove that it isn’t prime. So we will be stuck with at least half of the points left up to the fate of the factor sums, if not for a more powerful trick…
Fermat
Fermat numbers are those of the form 2k + 1. As before, we know a lot about these numbers and when they can be prime. However, the story is quite a lot different from Mersenne.
Specifically, a Fermat number 2n + 1 will always be divisible by 2a + 1, where a is the largest power of two dividing n. Even if that power of two is 20 = 1, the divisor 220 + 1 = 3 is nontrivial! You can confirm that every odd power of two, plus one, is a multiple of 3.
The only numbers left that could be Fermat primes, are 22n + 1. This is a sequence that grows incredibly fast. The first 5 numbers are known to be prime: 3, 5, 17, 257, 65537. The next 28 numbers are known to be composite, as well as scattered larger examples. We don’t know of any other Fermat primes, and there’s a reasonable argument that they are always composite after n = 5 (though no proof).
Similarly to above, we look at the GCD to prove s‘ – 4 composite, but this time it’s GCD(s + 4, 2k + 1). The same style of argument, but with the signs flipped. If s + 4 shares factors with a bunch of Fermat numbers, then all of the corresponding k won’t ever be green.
In practice
Let’s start with the simplest example again: 220 + 1 = 3. The interesting factor is still 3, but the k is now 20 = 1, which was out of reach for Mersenne. This has the potential to be way more powerful, since it covers the most frequent type of point. Whenever s + 4 is a multiple of 3 (which is a different collection of sums than those where s – 4 is a multiple of 3), we eliminate k = 1 from possibly being green. And by the Fermat divisor rule, we also eliminate k = 3, 5, 7, and every odd number.
These lines are even more bare than we would expect. The only green point with any value of k that was visible at one point in the video above, was (112, 13), which has k = 4. (But note that it isn’t a solution – F(125) = 3 due to the additional green points (64, 61) and (109, 16) which were removed by b > 1).
But what happened to k = 2?
The curious case of k = 2
We can’t find a sum that is simultaneously 4 more than, and 4 less than, a multiple of 3. So at least in their simplest form, Fermat and Mersenne factors are incompatible with each other, meaning Mersenne can’t explain this. But it turns out that k = 2 has another trick, specific to 2.
Let s = a + 22b, where a and b are odd and greater than 1. One factor sum we haven’t considered already, is s” = 22 + ab. This is different from s‘, but it shares the feature that if we can prove it is in S, then our original coordinates are not a green point.
This one’s actually really easy. s” is odd, since ab is odd. As before, modular arithmetic can show that s” is only a multiple of 3 if s is a multiple of 3. And finally, when you subtract 4, you just get ab, the product of two odd numbers greater than 1. That’s always composite.
The three tails of the comet
With all of the above, we can separate S into three parts:
● s is divisible by 3
• we can’t rule out any points, since even our k = 2 trick doesn’t prove anything
● s is 1 more than a multiple of 3
• we can rule out all even k using the Mersenne factor 3
● s is 2 more than a multiple of 3
• we can rule out all odd k using the Fermat factor 3
• we can additionally rule out k = 2 using the trick above
Naively, all of the rest of the points “might or might not” be green, including those with b = 1 or b = a. But this already describes three well-separated portions of F(s). And if we plot them..

Bingo.
The Bottom Branch
While it feels good to describe the most visual feature of Freudenthal’s comet, we must remember that the solutions only happen when F(s) = 1. So let’s now ignore the top two branches, and look just at the bottom branch. s will now always be 2 more than a multiple of 3.
Very roughly, we can say a point is green in the bottom branch whenever
● It is (p, 2k), a prime and a power of two (in either order)
• Example: (16, 13)
• Note that for all s in the bottom branch, subtracting an odd power of two leaves a multiple of 3.
As a result, all prime-and-power-of-two points here, have powers of 4.
● It is (a, 2kb), where k ≥ 4 is even, and at least 4 different connected odd numbers are all prime
• Example: (112, 13) is green because the following 4 numbers are prime
◆ 13
◆ 112 / 24 = 7
◆ 24 + 13 × 7 – 4 = 103
◆ 24 × 13 + 7 – 4 = 211
This lets us predict asymptotic growth using the Prime Number Theorem. In short, every time you need n to be prime, divide the formula by log(n).
Formula for growth
As mentioned before, prime and power of two is rare enough to only contribute a constant expected number of green points, independent of s. We’ll call it C1.
For the cases like (112, 13), we have some dependence on s. I’ll use a bit of big-O notation here, which means “bounded by some multiple of”. Of the O(s) numbers that sit on the line, just about all of them can be written as (a, 2kb) with our constraints on b. We need four primes, so this type of point contributes O(s / log4(s)) to F(s).
Even though this is completely hand-wavy, we can say that the leading order growth of the bottom branch probably looks like F(s) ~ C1 + C2 s / log4(s) for constants C1 and C2.
Fitting the curve
I’ve taken the moving average of F(s) along the bottom branch, which makes it a lot less noisy. On top, I’ve put a very lazy curve fit where C1 = 2 and C2 = 1. For how much our methods are imprecise, the fit is pretty good..

Isn’t that still unbounded growth?
Correct! (112, 13) and green points like it, begin to crop up more and more, leading to lower likelihood of a solution as s gets higher. And this is where I will pose this blog post’s ultimate unsolved question.
Are there infinitely many solutions to the infinite impossible problem?
If the lowest branch of F(s) has unbounded growth, then when s gets absolutely massive, there will be O(s / log4(s)) green points on it, a similarly massive number. It is hard to believe that we will get F(s) = 1 infinitely many times, if the lowest branch grows in this way.
But at the same time, we are still rolling in solutions by the point my computer runs out of memory. If we look at a histogram of solutions by sum, it’s not clear whether it is slowing down:

Y axis: number of solutions in bin
It’s not sufficient to use this data to predict the infinite behavior of solutions!
So which is it?
Eliminating more k
It’s time to think about other values of k. If we can get rid of enough k, and prevent all their associated points from becoming green, then we can find lower branches of F(s). Remember that k is the number of powers of two in the even coordinate, so when we talk about something like k = 64, we are necessarily talking about sums that are at least 264. This is big enough that a computer won’t be happy working with it, so we need to be clever with our math.
Fermat and Mersenne, at the same time
There are other moduli besides 3 to use as our GCD. When either s + 4 or s – 4 is divisible by them, the growing part grows slower. By the Chinese remainder theorem, we can figure out an appropriate s for any combination of modular constraints, as long as all of the moduli are separate primes.
Now, if we try to include Mersenne factors, we will need a new one for every time k passes a prime. If we try to instead include Fermat factors, we will need a new one for every time k passes a power of two. Each one of these factors will make the congruence a little nastier. We definitely get more bang for our buck with Fermat.
However, it turns out that through a reasonably simple combination of both, we can get rid of every single k. Our goal is to simultaneously eliminate all k which are not a multiple of some factor d using Fermat factors, and all k which are a multiple of that same d, using Mersenne factors.
Is it that simple?
We’ve been thwarted by this before. We got rid of even k by ensuring s – 4 was a multiple of 3. And we got rid of odd k by ensuring s + 4 was a multiple of 3. These are not compatible; we need the moduli to be different in order to set up a congruence and find solutions.

With Fermat divisors, we can prune the allowable k down to multiples of larger and larger powers of 2. By having s + 4 be a multiple of both 3 and 5, all that remains are multiples of 4. If we put a factor of 17 into s + 4 as well, we are covered up to multiples of 8.
But consider the Mersenne number we would need to use, to get rid of multiples of 8. It’s 28 – 1, which is 255, and which factors as 3 × 5 × 17. There are no factors we can use, since they are all already spoken for. You can prove using induction and difference of squares, that 22n – 1 is always going to be the product of the first n – 1 Fermat numbers.
Saved by 641
Somewhat famously, 232 + 1 = 4294967297 can be factored as 641 × 6700417. This is the first composite Fermat number, a result first proven in 1732, many years after Fermat’s death, by the famous mathematician Euler.
The fact that 232 + 1 is composite means it is sufficient for s + 4 to be a multiple of either 641 or 6700417 to get rid of odd multiples of 32. And this leaves the other factor available!
264 – 1 is 3 × 5 × 17 × 257 × 641 × 65537 × 6700417. s + 4 has to be divisible by 6 of those factors in order to make it so that a point isn’t green unless its k is a multiple of 64. But the 7th can be put to use in Mersenne fashion. Let s – 4 be a multiple of whichever of 641 and 6700417 was not used already. We now have eliminated all k, while maintaining a valid congruence!

By the Chinese remainder theorem, there is an infinite sequence of integers which satisfy these requirements, and for all of them which are in S, we can make a powerful statement. They will never have any green points of the form (a, 2kb) with b > 1.
The actual progression
These s values are massive, the smallest using 641 for Mersenne is 6705290747541849491, and the smallest using 641 for Fermat is 30188197382697384551. In both progressions, to get to the next you add 2(264 – 1) = 36893488147419103230. But, it’s a linear progression, and as a side effect of the construction, all of the values are in S.
If you “zoom out” the number line far enough, these numbers are everywhere. When we restrict F(s) to these values, even without calculating anything explicitly, we have proven that almost every associated point cannot be green. We have fully quashed the leading order, and found a well-separated sub-branch below the ones at O(s/log4(s)). One that we would have never found by trying to compute F(s) using computer memory and algorithms.
What does this mean for the unsolved problem?
The Fermat and Mersenne factors define many arithmetic progressions, most of which are still O(s/log4(s)) but with extremely small constants. We have found at least one branch though, which cannot grow like that at all. Even the fact that such a branch exists, might help prove something useful about F(s).

However, we still aren’t very close to proving that F(s) = 1 infinitely often!
We left ourselves a laundry list of exceptions. Avoiding the case a = b is the same as saying that s isn’t divisible by Fermat numbers, which I think we’ve covered as a side effect of the congruence. s + 4 is, and so s itself won’t be. The case b = 1 is a little nastier since it can’t be avoided. There will always be points on any given line, with a power of two for one coordinate. But you can do a little bit of algebra, and show that for these s, subtracting a power of two gives a very familiar factor..
This leaves us running into a new problem.. Not only do we eliminate most green points, when a isn’t prime then we can’t guarantee any green points. We only have the “maybe” green points, and comparatively few of them. Perhaps F(s) = 0 for all of these s, which is not going to yield solutions.
If that is the case, perhaps the best way of finding solutions is actually to look at every branch that does shoot off to infinity, right as it starts to do so. Regardless, I’ve never taken this problem further, and I’ve never found a source that has either. Accordingly, this is where the blog post will end.
Summary
If you’ve made it this far, you’ve learned just about everything I know on this topic. I’d like to call attention to just how involved the journey has been.
We started with Freudenthal’s impossible problem, which was introduced as lines of dialogue between Alice, Sam and Polly. It was clear there was some number theory hiding, but we didn’t even need to use it to find our solution. Instead we just let a computer tell us which points on an imaginary grid survived each stage of the conversation.
By making the imaginary grid infinite, we started to actually do math. We started talking about primes and factors, and constructed the set S. Using this machinery, we suddenly had access to a beautiful graph: Freudenthal’s comet. What initially looked like 3 branches was actually a collection of sparser and sparser branches, defined by their relationship to Fermat and Mersenne numbers.
We have definitely lived up to Hans Freudenthal’s perspective of math. We’ve covered a lot of number theory topics that one might learn for learning’s sake. But we found and built them while chasing the answer to a problem, which makes them feel more real.
The Future
Someone might be able to develop other techniques, based loosely or entirely on my progress here. If you can use what I’ve put forward to prove or disprove the infinity of solutions, that’s everything I’ve ever wanted from this puzzle.
Separately, If you want to start from the beginning but using a lower bound of 2 or 4 instead, I’m glad I’ve inspired you!
No matter what you take away from this blog post, I’m glad you’ve read it. This has been a lot of fun to dig back up from my past, and organize with animations. I’m grateful to Grant from 3blue1brown for beginning the tradition of coaxing less-prolific math enthusiasts like me, into making informative content.